La Géométrie Sacrée: Histoire et Origine
Sur cette page, nous allons étudier ce que signifie le terme de géométrie sacrée et en quoi cette science nouvelle se distingue de la géométrie traditionnelle. Pour ce faire, comme vous en avez maintenant l'habitude avec moi, nous allons revenir à sa source, c'est-à-dire son origine. Vous allez voir que cette science ou ce concept est inscrit depuis longtemps dans les traditions anciennes.

Introduction
Nous avons tous appris au cours de notre cursus scolaire les principes de la géométrie ainsi que la façon dont on pouvait obtenir des formes géométriques à travers des mesures et des angles précis. On traçait ces formes sur une feuille en papier. Celles que nous connaissons le mieux sont le triangle, le carré, le rectangle et le cercle. Il y a aussi d'autres formes un peu moins connues qui revêtent une importance singulière comme le pentagone, l'hexagone, l'octogone ou le décagone. Ces formes géométriques sont dites bidimensionnelles (à deux dimensions) en raison de leur manque de profondeur. Néanmoins, malgré le support limité que représente la feuille en papier pour générer des formes géométriques, il est possible de créer des formes tridimensionnelles (à trois dimensions) en jouant sur les couleurs, les contrastes et la profondeur. Vous devez probablement connaitre certaines de ces formes géométriques puisqu'on les a dessinées un jour ou l'autre en classe de mathématiques. Je peux ainsi vous citer: le cube, la pyramide, le cylindre, la sphère ou le cône. Comme nous allons le voir par la suite, de nombreux autres polyèdres (formes géométriques tridimensionnelles) existent et certains d'entre eux sont fondamentaux pour comprendre la façon dont notre univers est fait.
Certaines figures bidimensionnelles, notamment le triangle et le rectangle, peuvent adopter plusieurs formes différentes. Dans la famille des triangles, on retrouve le triangle équilatéral, caractérisé par trois côtés de même longueur et trois angles égaux. Etant donné que la somme de ses angles internes est égale à 180°, nous obtenons l'opération arithmétique suivante: 60*3 = 180°. Ainsi, chaque angle de ce triangle est de 60°. Retenez ce nombre, j'y reviendrais plus tard. Ensuite, nous avons le triangle isocèle qui possède deux côtés égaux et un troisième côté plus court ou plus long. De même, il possède deux angles internes similaires et un troisième angle plus fermé ou plus ouvert en fonction de la longueur du troisième côté. Les deux angles égaux varient en fonction de la valeur du troisième angle. Il existe plusieurs sortes de triangle isocèle dont le triangle d'or. Le troisième triangle que je vais aborder ici, vous le connaissez aussi très bien puisque nous l'appelons triangle rectangle. Ce dernier triangle est le plus important des trois, pour une raison que je développerais plus tard. Nous avons normalement tous appris à le dessiner en nous appuyant sur le théorème de Pythagore (à part si vous n'avez jamais été en école publique, ce qui est assez rare). Ce triangle a la particularité de générer un angle droit entre deux de ses côtés. Pour rappel, un angle droit est un angle de 90° créé par deux droites perpendiculaires (une droite horizontale et une droite verticale). Il existe d'autres styles de triangles mais ceux-ci sont secondaires, je ne parlerais donc pas d'eux dans cet article.
Ensuite, en ce qui concerne les rectangles (du latin "rectus angulus", "rectus": "droit" et "angulus": "angle"), nous pouvons dire qu'ils sont de taille variable et qu'ils ont tous quatre angle droits. Un rectangle avec une longueur égale à sa largeur est un carré. Un rectangle dont la longueur vaut le double de sa largeur est un bicarré (ou double carré). Un rectangle dont la longeur vaut le triple de sa largeur est un tricarré (ou triple carré) etc... Nous pouvons aussi citer le rectangle d'or qui possède la particularité d'avoir un côté dont la valeur est celle du nombre d'or, à savoir environ 1.618 (c'est un nombre irrationnel ou infini) et un autre côté valant un. La version polyédrique d'un rectangle est ce qu'on appelle un parallélépipède rectangle. Par exemple, la chambre du roi de la Grande Pyramide est un parallélépipède rectangle suivant les dimensions du bicarré avec comme unité de mesure la coudée royale égyptienne de 52.36 cm au sol. Ainsi, sa largeur vaut 5.236 mètres et sa longeur exactement le double, à savoir 10.472 mètres (10 coudées de large sur 20 coudées de long).
Plusieurs types de triangles


formes géométriques plates (bidimensionnelles)
formes géométriques avec du volume (tridimensionnelles)

Origine
Nous avons souvent tendance à croire que les règles de la géométrie sont apparues avec le théorème de Pythagore. Cependant, si l'on s'intéresse de plus près à la recherche archéologique, on s'aperçoit qu'une ancienne tablette cunéiforme sumérienne du nom de Plimpton 322 énonce déjà plusieurs siècles auparavant les mêmes principes de géométrie qu'enseignera plus tard Pythagore. De plus, si l'on se réfère au travail passionnant du chercheur indépendant Howard Crowhurst, ainsi qu'à celui d'autres chercheurs qui se sont inspirés de lui, il semblerait que les civilisations du Néolithique connaissaient et maitrisaient eux aussi la géométrie. En effet, en étudiant pendant près de trente ans la disposition et le rôle des mégalithes bretons, Howard s'est rendu compte qu'ils reprenaient les règles du théorème de Pythagore. En plus de cela, il a découvert que ces relations géométriques étaient relatives à l'astronomie, c'est-à-dire à la position du Soleil, de la Lune et de certaines étoiles dans le ciel nocturne. Si vous ne connaissez pas encore son travail, je vous recommande vivement d'aller visionner le film récapitulant toutes les découvertes qu'il a faites à travers ses recherches, sorti l'année dernière et disponible gratuitement sur la chaine Youtube "Epistemea". Le nom du film est "Mégalithes, Un Monde Oublié". Howard a repris puis poursuivi le travail débuté quelques décennies plus tôt par Alexander Thom qui s'était rendu compte qu'une unité de mesure (le yard mégalithique) avait été employée pour placer chaque mégalithe les uns par rapport aux autres ainsi que dans le diamètre des cromlech (cercles de pierre).

Tablette Plimpton 322
Si l'on s'oriente maintenant vers l'Egypte, nous savons qu'il existe une multitude de temples et de pyramides ayant été construits dans ce pays. L'archéologue Flinders Petrie a mesuré les dimensions de toutes les pyramides du plateau de Gizah et a aussi décelé plusieurs unités de mesure que les égyptiens ont utilisé pour les construire. Le chercheur indépendant Quentin Leplat a repris son travail, en s'appuyant rigoureusement sur les mesures que l'archéologue anglais a pris soin de noter dans ses carnets de recherche et de voyage, et s'est rendu compte que l'ensemble du plateau suivait les principes de la géométrie modulaire avec grande précision. De même, aux Etats-Unis, le chercheur indépendant Robert Edward Grant, qui serait la réincarnation de Pythagore et de Léonard de Vinci, a réussi à inclure chaque pyramide et leurs dimensions précises dans un schéma tout aussi précis s'appuyant sur certaines figures de la géométrie sacrée dont je vais parler d'ici peu. Il en a fait la démonstration dans une courte série de vidéos sur sa chaine Youtube. Pour revenir en France, les chercheurs George Vermard et Mathieu Lavaux ont réalisé une série de 60 diaporamas sur leur site internet où ils expliquent que les dimensions de la Grande Pyramide sont à mettre en relation avec la dimension du Soleil, de la Lune et des autres planètes de notre Système Solaire. Pour ceux d'entre vous qui n'aurais pas entendu parler de leur travail par le passé, cela pourrait être un choc, mais chaque mesure a été vérifiée, ce qui nous informe du niveau intellectuel qu'avait les égyptiens bien avant Pythagore.
Au Mexique, on retrouve aussi des pyramides massives qui auraient été construites par les Mayas il y a plusieurs milliers d'années. Le complexe de Teotihuacan et la pyramide de Kukulcan à Chichen Itza en sont les plus grands représentatifs. Selon l'auteur roumain Radu Cinamar, le complexe de Teotihuacan remonterait à environ 30 000 ans. Si vous voulez en savoir plus, vous pouvez aller télécharger et consulter gratuitement la traduction française que j'ai faite de son livre sur ma chaine Youtube ou en m'envoyant un mail à l'adresse mail indiquée sur mon site. Ainsi, les dimensions de chaque pyramide de Teotihuacan ont été réalisé avec minutie et les résultats qui en ressortent sont tout aussi impressionnant que pour les pyramides de Gizah. Il semblerait même que Teotihuacan ait servi de modèle pour la réalisation du plan architectural du plateau de Gizah.

Complexe de Teotihucan
Géométrie traditionnelle
Il y a encore quelques décennies, on utilisait la géométrie pour réaliser des plans architecturaux accompagnés de mesures afin d'accomplir un objectif pratique: plan d'une maison, d'un immeuble, placement des routes et des bâtiments dans une ville, etc... Dans le milieu scientifique, la géométrie représentait un moyen d'illustrer des formules mathématiques, qu'elles soient simples ou complexes, sous la forme de figure géométrique, de schéma ou de dessin. Dans l'art, elle permettait au peintre de répartir de façon précise les différents éléments qu'il souhaitait inclure dans sa toile ainsi que d'orienter le regard du spectateur dans une direction voulue à travers des lignes de fuite. C'est ce qu'on appelle la perspective empirique et la perspective linéaire. La perspective empirique consiste à donner de la profondeur à une toile tout en dirigeant l'attention du spectateur vers plusieurs points de fuite choisis par le peintre. Quant à la perspective linéaire, on sait qu'elle fut théorisée par Giovanni Battista Alberti dans son livre De Pictura lors de la Renaissance italienne et qu'elle consiste non plus à construire une toile sur plusieurs points de fuite mais sur un point de fuite unique, placé sur une ligne d'horizon. En archéologie, il existe un domaine d'étude, appelé la topographie, dont l'objectif est de reconstituer la forme et les dimensions d'un site de fouille afin que l'archéologue puisse avoir une vision d'ensemble des types de structure qui se trouvaient là auparavant et quelle avait bien pu être leur fonction. Ce travail est facilité par la photogrammétrie et les logiciels de reconstitution 3D. Maintenant que vous comprenez mieux à quoi je me réfère quand je parle de géométrie "traditionnelle", je vais pouvoir passer à la suite et entrer dans le domaine de la géométrie dite "sacrée".
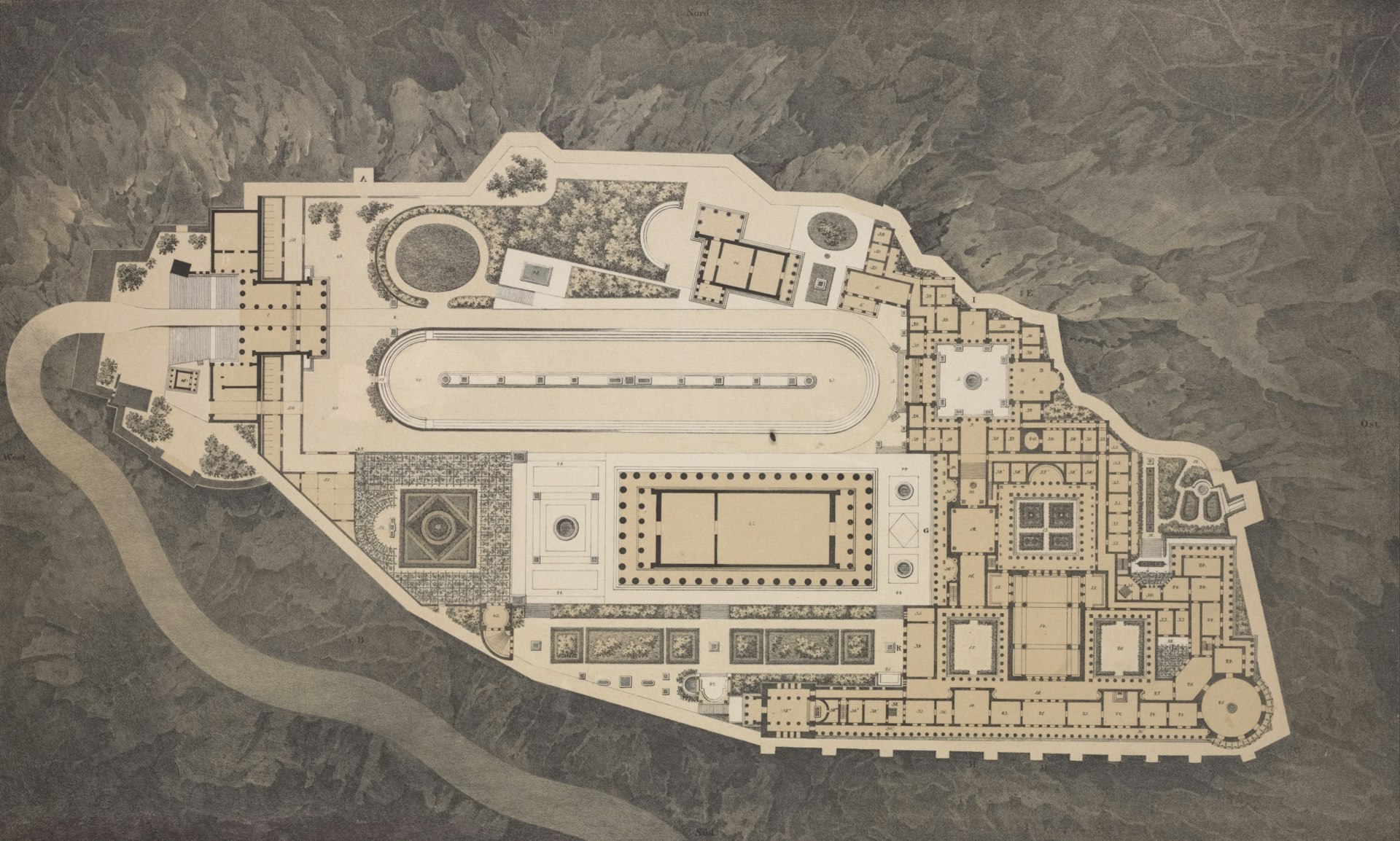
Plan d'une cité grecque
Dans le même temps, des formes géométriques anciennes furent redécouvertes et servirent de support pour assimiler cette nouvelle notion. Parmi celles-ci, je peux vous citer la graine de vie, le fruit de vie, la fleur de vie, la merkaba et le cube de Métatron. La plupart d'entre elles ont été compilé dans le livre de Drunvalo Melchizedek appelé l'Ancien Secret de la Fleur de Vie qui sortit en juin 1996. Cet homme a pu voir lors d'un voyage en Egypte, que la fleur de vie était inscrite sur une pierre de l'Osireion, grande enceinte situé à l'arrière du temple de Sethy 1er à Abydos. Les égyptiens de l'Antiquité en avait donc connaissance. Cette nouvelle manière d'envisager la géométrie fut renforcé par un changement de conscience à l'échelle collective. De plus en plus de personnes se sont mises à méditer, faire du yoga ou réciter des mantras ainsi qu'à exploiter les propriétés curatives des pierres et des huiles essentielles. De nos jours, je pense que la géométrie sacrée est autant considéré que la géométrie traditionnelle. Des recherches plus récentes, nous montre que des sons peuvent créer des formes géométriques en fonction de la fréquence à la quelle ils sont associés, c'est l'art de la cymatique. Je développerais un peu plus ce point dans mon article sur la musique. Dans le même temps, des scientifiques testèrent leur appareil électromagnétique à proximité ou à l'intérieur de polyèdres comme des pyramides, des cubes, des demi-sphères ou des parallélépipèdes rectangles et se sont rendus compte que la forme géométrique produisait une fréquence inaudible mais détectable qui pouvait agir sur nos cellules et nos neurones, c'est ce qu'on appelle l'onde de forme. Cet effet peut être accentué ou diminué en fonction des influences cosmotelluriques du lieu où se trouve cette forme géométrique. Elle tient alors compte de l'astrologie (impact de l'énergie des astres sur nos corps) et de la géobiologie (impact des ondes telluriques sur nos corps).
Géométrie sacrée
Ces dernières décennies, les formes géométriques ont pris une nouvelle dimension. On ne les considère plus uniquement sous un prisme fonctionnel, utililtaire ou pratique mais comme un moyen de conceptualiser la Nature et l'Univers. De nombreux chercheurs indépendants issus de métiers très variés, allant de la biologie à l'astrophysique, ce sont rendus compte que nos corps, le vivant, les planètes, les étoiles et les galaxies sont créés d'une imbrication de formes géométriques qui leur permettent d'avoir une apparence matérielle. Sans géométrie matérielle, rien n'existe (du moins pas dans le milieu physique). Ce changement de perspective lui valut ce nom de sacré. La géométrie n'est ainsi plus à considérer comme le résultat d'un calcul mathématique mais comme la source créatrice de notre réalité.
Cellule géométrique


Fleur de vie
Les cinq solides de Platon
Maintenant que vous savez ce que signifie la géométrie sacrée, je vais vous parler de cinq solides qui prennent de plus en plus d'importance à notre époque pour expliquer la nature de notre réalité. Je vais les disséquer pour vous les uns après les autres, puisqu'ils sont centraux, dans une théorie que j'ai élaboré à partir de la fleur de vie, pour expliquer la transition entre le système sexagésimal sumérien et le système décimal pythagoricien, comme je l'ai expliqué dans mon article sur l'histoire de l'astronomie. Ces cinq solides, nous les connaissons sous les noms de tétraèdre, hexaèdre (cube), octaèdre, icosaèdre et dodécaèdre. Ils ont été en partie découvert à l'époque de Pythagore mais furent vraiment mentionné de manière plus exhaustive dans le Timée de Platon. Le tétraèdre est un polyèdre constitué de quatre faces triangulaires ("tétra" veut dire "quatre"). Chaque triangle est équilatéral. Comme nous l'avons vu avant, les angles internes d'un triangle équilatéral sont de 60°. Cependant, cette fois-ci, nous avons quatre triangles, ce qui signifie que nous devons multiplier nos 180° par quatre. Ainsi, la valeur totale des angles de ce polyèdre est égal à 720°. Il possède six arêtes. Pour finir, Platon a associé chacun de ses solides à un des cinq éléments de la nature. Ainsi, le tétraèdre correspond à l'élément feu. Pour l'anecdote, en explorant l'archipel de Malte avec Google Earth, j'ai découvert qu'il existait une église de style tétraédrique sous sa forme de patron. J'ai d'abord pensé à une sorte de Tetractys de Pythagore, avant de me rendre compte plus récemment qu'en réalité c'est un des solides de Platon. A ma connaissance, c'est la seule église de cette sorte qui existe dans le monde. Si vous voulez en savoir plus sur mes découvertes à Malte, j'ai sorti une série de vidéos sur ma chaîne Youtube qui fait référence à cela.

Caractéristiques des cinq solides de Platon